Difference between revisions of "CFD"
NikLebedenko (talk | contribs) (Added equations to continuity equation) |
NikLebedenko (talk | contribs) (Added more equations) |
||
| Line 13: | Line 13: | ||
* How to write simultaneous equations as matrices, and | * How to write simultaneous equations as matrices, and | ||
* What a vector is. | * What a vector is. | ||
TODO: | |||
* Make the equation derivation more consistent with real CFD solvers (symmetric matrix, non-zero RHS) | |||
* Add more links at the bottom | |||
* Get someone to read through it and point out poorly-explained things | |||
Every CFD solver works by splitting up the region of interest (a process called "meshing" the "domain") into a bunch of small boxes (called the "cells" in the "mesh"), and solving a set of equations in each of those cells, taking into account how the flow variables (velocity, temperature, pressure) are related between neighbouring cells. Most commonly: | Every CFD solver works by splitting up the region of interest (a process called "meshing" the "domain") into a bunch of small boxes (called the "cells" in the "mesh"), and solving a set of equations in each of those cells, taking into account how the flow variables (velocity, temperature, pressure) are related between neighbouring cells. Most commonly: | ||
| Line 41: | Line 46: | ||
If we assume an "incompressible" (constant density) fluid, e.g. water, we can divide by the density term <math>\rho</math> on both sides. If we assume a "steady" flow, then nothing changes with time, i.e. all time derivatives are zero. The equation becomes | If we assume an "incompressible" (constant density) fluid, e.g. water, we can divide by the density term <math>\rho</math> on both sides. If we assume a "steady" flow, then nothing changes with time, i.e. all time derivatives are zero. The equation becomes | ||
<math>0 = ({\rho}UA)_{wc} - ({\rho}UA)_{ce}</math> | <math>0 = ({\rho}UA)_{wc} - ({\rho}UA)_{ce}</math> | ||
| Line 47: | Line 53: | ||
Take a moment to predict what our solution to this velocity equation will look like, given these assumptions. | Take a moment to predict what our solution to this velocity equation will look like, given these assumptions. | ||
At the moment, we are using values of velocity at the faces between the cells. But in a CFD solver, we only store the values at the cell centroid. The process of calculating face values using cell values on either side of the face is called interpolation. The most obvious interpolation "scheme" (method) is linear interpolation - that is, assume that all variables vary linearly between two points, as in the image above. We can also divide by the area of the faces, since both faces have the same area. The continuity equation becomes | At the moment, we are using values of velocity at the faces between the cells. But in a CFD solver, we only store the values at the cell centroid. The process of calculating face values using cell values on either side of the face is called interpolation. The most obvious interpolation "scheme" (method) is linear interpolation - that is, assume that all variables vary linearly between two points, as in the image above. We can also divide by the area of the faces, since both faces have the same area. The continuity equation becomes | ||
<math>0 = \frac{U_w + U_c}{2} \cdot A_{wc} - \frac{U_c + U_e}{2} \cdot A_{ce}</math> | <math>0 = \frac{U_w + U_c}{2} \cdot A_{wc} - \frac{U_c + U_e}{2} \cdot A_{ce}</math> | ||
| Line 100: | Line 107: | ||
=== The momentum equation === | === The momentum equation === | ||
In a similar process to the continuity equation, we can convert "F=ma but for fluids" into an actual equation, with the intermediate equation: rate of change of momentum at any point = rate of momentum flow in - rate of momentum flow out. For an arbitrary cell C experiencing pressure forces and an external force F, we can write | In a similar process to the continuity equation, we can convert "F=ma but for fluids" into an actual equation, with the intermediate equation: rate of change of momentum at any point = rate of momentum flow in - rate of momentum flow out. For an arbitrary cell C experiencing pressure forces and an external force F, noting that | ||
<math>UA = </math> the rate of flow of volume through a face, and | |||
<math>\frac{mU}{V} = \frac{\rho U V}{V} = \rho U = </math> the momentum per unit volume of fluid, we can write | |||
<math>\frac{\partial (\rho V U)_c}{\partial t} = ({\rho}UUA)_{wc} - ({\rho}UUA)_{ce} + (pA)_{wc} - (pA)_{ce} + F</math> | |||
Next we apply the assumptions of steady incompressible flow, zero external force, uniform face areas, as well as linear interpolation of pressure. | |||
<math>0 = ({\rho}UUA)_{wc} - ({\rho}UUA)_{ce} + (pA)_{wc} - (pA)_{ce} + F</math> | |||
<math>0 = (UUA)_{wc} - (UUA)_{ce} + \frac{(pA)_{wc}}{\rho} - \frac{(pA)_{ce}}{\rho} + \frac{F}{\rho}</math> | |||
<math>0 = (UUA)_{wc} - (UUA)_{ce} + \frac{(pA)_{wc}}{\rho} - \frac{(pA)_{ce}}{\rho}</math> | |||
<math>0 = (UU)_{wc} - (UU)_{ce} + \frac{p_{wc}}{\rho} - \frac{p_{ce}}{\rho}</math> | |||
Note that we have already found the velocity is the same everywhere, but that result is rarely true. Nonetheless, | |||
<math>0 = \frac{p_{wc}}{\rho} - \frac{p_{ce}}{\rho}</math> | |||
<math>0 = \frac{p_w + p_c}{2\rho} - \frac{p_c + p_e}{2\rho}</math> | |||
<math>0 = p_w - p_e</math> | |||
Note the term p/rho | Note the term <math>p/\rho</math> is sometimes called the "kinematic pressure", and is sometimes what the CFD software (e.g. OpenFOAM) will confusingly call p. So when finding the pressure drop when using an incompressible fluid, you may have to multiply by density. The best way to check whether you need to multiply by density, is to look at the units of p that the CFD software gives you. Ordinary pressure has units <math>kgm^{-1}s^{-2}</math>, while kinematic pressure has units <math>m^{2}s^{-2}</math>. | ||
For a more complete equation, you would also include the effects of viscosity and turbulence in this equation (added to the force F) | For a more complete equation, you would also include the effects of viscosity and turbulence in this equation (added to the force F). For simplicity, we will neglect viscosity and turbulence. | ||
By applying the boundary conditions of zero pressure gradient on the left boundary, and a fixed pressure of 0 on the right boundary, we arrive at these equations | By applying the boundary conditions of zero pressure gradient on the left boundary, and a fixed pressure of 0 on the right boundary, we arrive at these equations | ||
* Cell 1: <math>0 = p_1 - \frac{p_1 + p_2}{2}</math> | |||
* Cell 2: <math>0 = p_3 - p_1</math> | |||
* Cell 3: <math>0 = p_4 - p_2</math> | |||
* Cell 4: <math>0 = \frac{p_3 + p_4}{2} - 0</math> | |||
We now have a set of four simultaneous equations to solve for four unknowns (the pressure at each cell centroid), and we can solve this now, and find that the pressure everywhere is 0 Pa. Hooray! | We now have a set of four simultaneous equations to solve for four unknowns (the pressure at each cell centroid), and we can solve this now, and find that the pressure everywhere is 0 Pa. Hooray! | ||
| Line 124: | Line 157: | ||
* In 2D, we must also solve for velocity in the y direction. For this, we will apply conservation of momentum in the y axis (note that we will also solve the x-momentum equation for the x-velocity as well). | * In 2D, we must also solve for velocity in the y direction. For this, we will apply conservation of momentum in the y axis (note that we will also solve the x-momentum equation for the x-velocity as well). | ||
* Similarly in 3D, we need to solve the momentum equation in all three axes: x, y, and z to obtain the components of velocity in each direction. | * Similarly in 3D, we need to solve the momentum equation in all three axes: x, y, and z to obtain the components of velocity in each direction. | ||
* The momentum equation can be generalised to work in arbitrary dimensions - the process isn't important for now, although you should know that the spatial derivatives (e.g. partial | * The momentum equation can be generalised to work in arbitrary dimensions - the process isn't important for now, although you should know that the spatial derivatives (e.g. <math>\frac{\partial}{\partial x}</math>) are written with different notation, resulting in some terms called the "gradient", the "divergence", and the "laplacian" of a variable. A nice summary of these operations can be found at this link [todo]. | ||
=== Viscosity and turbulence === | === Viscosity and turbulence === | ||
| Line 167: | Line 200: | ||
== Step-by-step instructions == | == Step-by-step instructions == | ||
'''''IMPORTANT:''''' Although I include the links to the official websites for Ubuntu installation instructions, I recommend you <u>follow my instructions for installation</u> (unless you are a masochist), since the official instructions contain some mistakes and omissions. | '''''IMPORTANT:''''' Although I include the links to the official websites for Ubuntu installation instructions, I recommend you <u>follow my instructions for installation</u> (unless my instructions no longer work, or you are a masochist), since the official instructions contain some mistakes and omissions. | ||
=== Install Ubuntu === | === Install Ubuntu === | ||
Revision as of 18:15, 4 January 2022
This page is currently a work in progress by Nik Lebedenko - if you want to ask questions / see a mistake / request more details to be added to this page, feel free to email me or message me on slack.
Computational Fluid Dynamics (CFD) is the process of solving fluid mechanics equations with the use of computers. Think F=ma, but like... more. (I will elaborate further)
Crash course on the Finite Volume Method (FVM)
This section is incomplete
There are many resources for learning how CFD works properly (hopefully linked below, TODO), but you're not here for that. This section is designed for people who are doing a CFD simulation for just a one-time thing, and they can treat it like a black box that gives them answers (that is how I started). So, here are the bare minimum requirements for understanding roughly what is going on in any CFD solver. Nonetheless, I will assume you know:
- Some basic high-school physics about gases (e.g. what is pressure, how does it change with temperature)
- What a partial derivative is,
- What simultaneous equations are,
- How to write simultaneous equations as matrices, and
- What a vector is.
TODO:
- Make the equation derivation more consistent with real CFD solvers (symmetric matrix, non-zero RHS)
- Add more links at the bottom
- Get someone to read through it and point out poorly-explained things
Every CFD solver works by splitting up the region of interest (a process called "meshing" the "domain") into a bunch of small boxes (called the "cells" in the "mesh"), and solving a set of equations in each of those cells, taking into account how the flow variables (velocity, temperature, pressure) are related between neighbouring cells. Most commonly:
- The continuity equation: mass is not created or destroyed (conservation of mass).
- The momentum equation: "F=ma" but for fluids (conservation of momentum).
- The energy equation: energy is not created or destroyed (conservation of energy).
The continuity equation
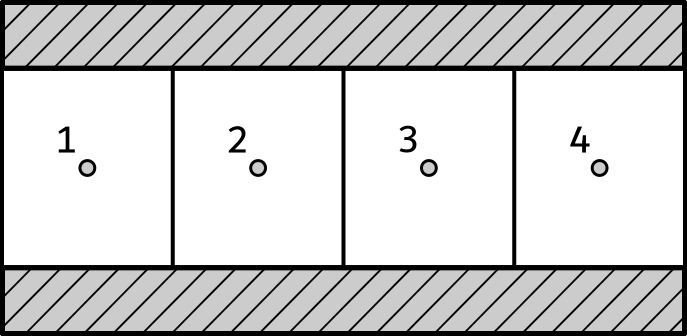
To clarify this, consider the example below of a simple two-dimensional pipe, image left. Now, let us "mesh" the "domain" into four "cells" (split the pipe into 4 boxes), image right.
Consider an arbitrary cell within this mesh labelled "C", with its western and eastern neighbours labelled "W" and "E" respectively. The faces between W & C and C & E are labelled WC and CE. The following abbreviations for variables will be used:
- X: Position,
- [math]\displaystyle{ \rho }[/math] (rho): Density,
- p: Pressure,
- U: Velocity (in the x-axis),
- V: Volume of the cell,
- A: Area of a face,
- Any variable with a subscript corresponds to the value of that variable at that location. E.g. UW is the velocity of the fluid at W. The area of face WC is AWC.
The continuity equation tells us that mass is not created or destroyed - said in another way, rate of change of mass at any point = rate of mass flow in - rate of mass flow out. For an arbitrary cell C, knowing that the mass flow rate through a given face is [math]\displaystyle{ {\rho}UA }[/math], we can write
[math]\displaystyle{ \frac{\partial (\rho V)_c}{\partial t} = ({\rho}UA)_{wc} - ({\rho}UA)_{ce} }[/math]
If we assume an "incompressible" (constant density) fluid, e.g. water, we can divide by the density term [math]\displaystyle{ \rho }[/math] on both sides. If we assume a "steady" flow, then nothing changes with time, i.e. all time derivatives are zero. The equation becomes
[math]\displaystyle{ 0 = ({\rho}UA)_{wc} - ({\rho}UA)_{ce} }[/math]
[math]\displaystyle{ 0 = (UA)_{wc} - (UA)_{ce} }[/math]
Take a moment to predict what our solution to this velocity equation will look like, given these assumptions.
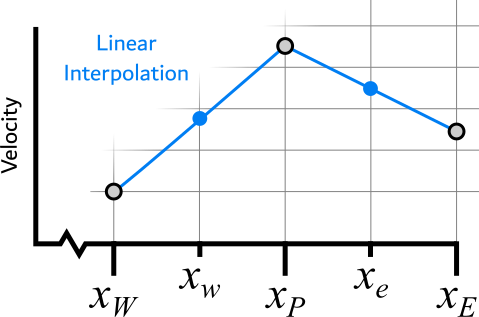
At the moment, we are using values of velocity at the faces between the cells. But in a CFD solver, we only store the values at the cell centroid. The process of calculating face values using cell values on either side of the face is called interpolation. The most obvious interpolation "scheme" (method) is linear interpolation - that is, assume that all variables vary linearly between two points, as in the image above. We can also divide by the area of the faces, since both faces have the same area. The continuity equation becomes
[math]\displaystyle{ 0 = \frac{U_w + U_c}{2} \cdot A_{wc} - \frac{U_c + U_e}{2} \cdot A_{ce} }[/math]
[math]\displaystyle{ 0 = \frac{U_w + U_c}{2} - \frac{U_c + U_e}{2} }[/math]
[math]\displaystyle{ 0 = \frac{U_w}{2} - \frac{U_e}{2} }[/math]
[math]\displaystyle{ 0 = U_w - U_e }[/math]
We can now apply this equation for cells 2 and 3. However, we can't apply this equation to cells 1 and 4, since they are both missing a neighbour (as they are on the boundary of the domain). Without knowing what the value of U is at the boundaries, we cannot solve (or even fully write down) the continuity equation. Therefore we must apply some special treatment at the boundaries (called boundary conditions) in order to solve this issue. Boundary conditions are specified by the CFD user. For the moment, we will use these boundary conditions:
- Flow velocity on the left boundary is fixed at 5 m/s (called a Dirichlet boundary - mnemonic: kind of sounds like "directly").
- Flow velocity on the right boundary is the same as the flow velocity at cell 4 (also known as a zero gradient condition, or von Neumann boundary).
Applying these conditions, we can now write down equations for cells 1 and 4, as well as the equations for cells 2 and 3 as found before.
- Cell 1: [math]\displaystyle{ 0 = 5 - \frac{U_1 + U_2}{2} }[/math]
- Cell 2: [math]\displaystyle{ 0 = U_3 - U_1 }[/math]
- Cell 3: [math]\displaystyle{ 0 = U_4 - U_2 }[/math]
- Cell 4: [math]\displaystyle{ 0 = \frac{U_3 + U_4}{2} - U_4 }[/math]
We now have a set of four simultaneous equations to solve for four unknowns (the velocity at each cell centroid). We can solve this now, and find that the velocity everywhere is 5 m/s. Hooray!
Let us simplify the notation a bit using matrices and vectors.
[math]\displaystyle{ \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \end{bmatrix} = \begin{bmatrix} 5 \\ 0 \\ 0 \\ 0 \end{bmatrix} - \begin{bmatrix} 0.5 & 0.5 & 0 & 0 \\ 1 & 0 & -1 & 0 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 0.5 & -0.5 \end{bmatrix} \begin{bmatrix} U_1 \\ U_2 \\ U_3 \\ U_4 \end{bmatrix} }[/math]
[math]\displaystyle{ \begin{bmatrix} 0.5 & 0.5 & 0 & 0 \\ 1 & 0 & -1 & 0 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 0.5 & -0.5 \end{bmatrix} \begin{bmatrix} U_1 \\ U_2 \\ U_3 \\ U_4 \end{bmatrix} = \begin{bmatrix} 5 \\ 0 \\ 0 \\ 0 \end{bmatrix} }[/math].
Abbreviated with a matrix of coefficients M, a solution vector U, and a right-hand-side vector B:
[math]\displaystyle{ \boldsymbol{MU=B} }[/math], where [math]\displaystyle{ \boldsymbol{M}= \begin{bmatrix} 0.5 & 0.5 & 0 & 0 \\ 1 & 0 & -1 & 0 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 0.5 & -0.5 \end{bmatrix} }[/math], [math]\displaystyle{ \boldsymbol{U} = \begin{bmatrix} U_1 \\ U_2 \\ U_3 \\ U_4 \end{bmatrix} }[/math], and [math]\displaystyle{ \boldsymbol{B} = \begin{bmatrix} 5 \\ 0 \\ 0 \\ 0 \end{bmatrix} }[/math]
We could now invert the matrix [math]\displaystyle{ \boldsymbol{M} }[/math], and calculate the solution vector [math]\displaystyle{ \boldsymbol{U} }[/math] using [math]\displaystyle{ \boldsymbol{U=M^{-1}B} }[/math]. The matrix [math]\displaystyle{ \boldsymbol{M} }[/math] always has size n x n, where n is the number of cells in the mesh (in this case 4). But typical CFD cases will have n in the thousands or millions - inverting matrices of this size becomes very time consuming. So instead, CFD solvers use an iterative approach on the equation [math]\displaystyle{ \boldsymbol{MU=B} }[/math], where they start with a guess for [math]\displaystyle{ \boldsymbol{U} }[/math], and improve their guess with successive iterations of an algorithm until the solution vector [math]\displaystyle{ \boldsymbol{U} }[/math] is "close enough" (this threshold is determined by the CFD user). The error in a solution for a variable is characterised by the "residual". A small residual means the solution has only a small error, and vice versa. The CFD user specifies what residual value qualifies as "close enough".
Important note, the solution vector [math]\displaystyle{ \boldsymbol{U} }[/math] does not store the components of velocity, i.e. [math]\displaystyle{ U_x, U_y, U_z }[/math], but instead stores the velocities at each cell centroid, i.e. [math]\displaystyle{ U_1, U_2, U_3, U_4 }[/math]. Indeed, the solution vector [math]\displaystyle{ \boldsymbol{U} }[/math] summarises the x-velocity at every point in our domain, while hypothetically the scalars [math]\displaystyle{ U_x, U_y, U_z }[/math] would only specify the 3D velocity at one point. Since we are currently only concerned with x-velocity, this might be more clear, but in higher dimensions it is important not to get confused.
The momentum equation
In a similar process to the continuity equation, we can convert "F=ma but for fluids" into an actual equation, with the intermediate equation: rate of change of momentum at any point = rate of momentum flow in - rate of momentum flow out. For an arbitrary cell C experiencing pressure forces and an external force F, noting that
[math]\displaystyle{ UA = }[/math] the rate of flow of volume through a face, and
[math]\displaystyle{ \frac{mU}{V} = \frac{\rho U V}{V} = \rho U = }[/math] the momentum per unit volume of fluid, we can write
[math]\displaystyle{ \frac{\partial (\rho V U)_c}{\partial t} = ({\rho}UUA)_{wc} - ({\rho}UUA)_{ce} + (pA)_{wc} - (pA)_{ce} + F }[/math]
Next we apply the assumptions of steady incompressible flow, zero external force, uniform face areas, as well as linear interpolation of pressure.
[math]\displaystyle{ 0 = ({\rho}UUA)_{wc} - ({\rho}UUA)_{ce} + (pA)_{wc} - (pA)_{ce} + F }[/math]
[math]\displaystyle{ 0 = (UUA)_{wc} - (UUA)_{ce} + \frac{(pA)_{wc}}{\rho} - \frac{(pA)_{ce}}{\rho} + \frac{F}{\rho} }[/math]
[math]\displaystyle{ 0 = (UUA)_{wc} - (UUA)_{ce} + \frac{(pA)_{wc}}{\rho} - \frac{(pA)_{ce}}{\rho} }[/math]
[math]\displaystyle{ 0 = (UU)_{wc} - (UU)_{ce} + \frac{p_{wc}}{\rho} - \frac{p_{ce}}{\rho} }[/math]
Note that we have already found the velocity is the same everywhere, but that result is rarely true. Nonetheless,
[math]\displaystyle{ 0 = \frac{p_{wc}}{\rho} - \frac{p_{ce}}{\rho} }[/math]
[math]\displaystyle{ 0 = \frac{p_w + p_c}{2\rho} - \frac{p_c + p_e}{2\rho} }[/math]
[math]\displaystyle{ 0 = p_w - p_e }[/math]
Note the term [math]\displaystyle{ p/\rho }[/math] is sometimes called the "kinematic pressure", and is sometimes what the CFD software (e.g. OpenFOAM) will confusingly call p. So when finding the pressure drop when using an incompressible fluid, you may have to multiply by density. The best way to check whether you need to multiply by density, is to look at the units of p that the CFD software gives you. Ordinary pressure has units [math]\displaystyle{ kgm^{-1}s^{-2} }[/math], while kinematic pressure has units [math]\displaystyle{ m^{2}s^{-2} }[/math].
For a more complete equation, you would also include the effects of viscosity and turbulence in this equation (added to the force F). For simplicity, we will neglect viscosity and turbulence.
By applying the boundary conditions of zero pressure gradient on the left boundary, and a fixed pressure of 0 on the right boundary, we arrive at these equations
- Cell 1: [math]\displaystyle{ 0 = p_1 - \frac{p_1 + p_2}{2} }[/math]
- Cell 2: [math]\displaystyle{ 0 = p_3 - p_1 }[/math]
- Cell 3: [math]\displaystyle{ 0 = p_4 - p_2 }[/math]
- Cell 4: [math]\displaystyle{ 0 = \frac{p_3 + p_4}{2} - 0 }[/math]
We now have a set of four simultaneous equations to solve for four unknowns (the pressure at each cell centroid), and we can solve this now, and find that the pressure everywhere is 0 Pa. Hooray!
Again, CFD solvers actually work with these equations in matrix form, and use an iterative approach to solve them, until the residual is below a threshold value set by the user.
The energy equation
In case we also wanted to find the temperature of the fluid throughout the domain, we could solve the energy equation: rate of change of energy at a given point = rate of energy flow in - rate of energy flow out. I will not go through the derivation here (although it's fairly simple) - it is enough to know that the CFD solver performs an iterative approach to solve for temperature using the conservation of energy until the residual is low enough.
In the case of an incompressible flow, this isn't necessary, since density is constant. But for a compressible flow, the density at a given location is a function of temperature, so it is necessary to find the temperature everywhere in the fluid, so that the density can be found.
Higher dimensions
- In 1D, we have been solving for velocity in the x direction by applying conservation of momentum in just one direction - the x axis.
- In 2D, we must also solve for velocity in the y direction. For this, we will apply conservation of momentum in the y axis (note that we will also solve the x-momentum equation for the x-velocity as well).
- Similarly in 3D, we need to solve the momentum equation in all three axes: x, y, and z to obtain the components of velocity in each direction.
- The momentum equation can be generalised to work in arbitrary dimensions - the process isn't important for now, although you should know that the spatial derivatives (e.g. [math]\displaystyle{ \frac{\partial}{\partial x} }[/math]) are written with different notation, resulting in some terms called the "gradient", the "divergence", and the "laplacian" of a variable. A nice summary of these operations can be found at this link [todo].
Viscosity and turbulence
We ignored the effects of viscosity, but this is straightforward to include in the momentum equation, simply by adding an extra force to the equation to account for viscosity.
We ignored turbulence in the momentum equation for this example, but real flows often exhibit turbulence ("random" fluctuations), especially at high speeds and low viscosities. Since the effect of turbulence is to increase mixing between layers, it can be modelled using a modified viscosity. This modified viscosity is the sum of the ordinary viscosity and the "turbulent viscosity" - this turbulent viscosity is calculated at every location in the mesh by a turbulence model. The turbulence models calculate some variables which quantify the turbulence at every location, and use those variables to calculate the turbulent viscosity. Some common turbulence models include (along with some broad pros & cons):
- K-epsilon model: best for use when the cells are quite large ("coarse") near the walls, and for preliminary simulations.
- K-omega model: requires smaller (finer) cells near the walls in order to work best. Generally more accurate than K-epsilon, but more computationally expensive, and requires a finer mesh. Is also more sensitive to boundary conditions than K-epsilon.
- K-omega SST (Shear Stress Transport) model: a combination of the K-epsilon and K-omega models, with an added shear stress transport model. Generally more accurate than K-omega and K-epsilon, but requires a finer mesh and is more computationally expensive than K-epsilon.
Stability tips
- CFD simulations can sometimes have variables blow up to infinity or show unphysical oscillations in the flow, if care is not taken with the setup process. The stability of a simulation (i.e. how likely it is to avoid blowing up) can be influenced by choice of numerical scheme, the quality of the mesh, and the selection of boundary conditions.
- In OpenFOAM, each operation has its own numerical scheme selection - for example:
- Interpolation (we used the linear scheme for this operation in the example above),
- Gradient,
- Divergence - this one is particularly influential to stability,
- Laplacian.
- Details on the selection of which scheme to use is beyond the scope of this section, but a good rule-of-thumb is that less accurate schemes (e.g. upwind interpolation) tend to be more stable, and vice versa. Gradient limiters can also be used to add stability at the expense of accuracy.
- Meshing is not as straightforward as shown here, especially with more complicated geometries. Sometimes, poor quality meshes can cause problems with the simulation. There are numbers that meshing software can calculate to represent the quality of a mesh (called a mesh quality metric).
- For example, meshes with orthogonal cells perform better than those with non-orthogonal cells. In our example, all the cells were perfectly orthogonal - that is, the faces were perpendicular to the lines between the adjacent cell centroids.
- How close the cells are to having perpendicular faces is called the "orthogonal quality" in ANSYS.
- In OpenFOAM, the opposite of this is given as the "non-orthogonality angle".
- Other examples include cell skewness (lower is better) and cell aspect ratio (closer to 1 is better). It is important to ensure these quality metrics are not too bad, otherwise the stability and accuracy of the simulation can be affected.
Further reading
Hopefully this section gives an understandable explanation of roughly what most CFD solvers do. If you want to explore the topics mentioned here in more detail, here are some resources that might help: [todo]
Fluid-structure interaction (FSI)
IMPORTANT: Although I hope that these instructions will be easily understood by anyone, this is not a beginner's project! If you want a proper introduction to CFD, this is not it. (I am in the process of creating a beginner's guide which will be available soon™)
This technique allows complex interactions between flexible structures and fluid flows. This has been used to predict fin flutter at hypersonic speeds for Griffin 1.
Simulations of this kind are achievable with the combination of the following free open-source software packages:
- OpenFOAM (website, install on Ubuntu) - a C/C++ library for the solution of fluid mechanics problems formulated with the Finite Volume Method (FVM),
- Important: there are two main versions of OpenFOAM, provided at OpenFOAM.com and OpenFOAM.org. I have only used the .com version, but everything here should also be possible with the .org version.
- FEniCS (website, install on Ubuntu) - a Python interface to the DOLFIN C++ library for the solution of solid mechanics problems formulated with the Finite Element Method (FEM), and
- preCICE (website, install on Ubuntu) - a very powerful library which allows the coupling of arbitrary solvers using human-readable syntax.
- Note: in order to use OpenFOAM and FEniCS with preCICE, it is also necessary to download their respective adapters. See this page for OpenFOAM and this page for FEniCS from the preCICE website for further information.
Step-by-step instructions
IMPORTANT: Although I include the links to the official websites for Ubuntu installation instructions, I recommend you follow my instructions for installation (unless my instructions no longer work, or you are a masochist), since the official instructions contain some mistakes and omissions.
Install Ubuntu
If you are running a Windows machine (Windows 10 or above), I recommend installing Windows Subsystem for Linux (WSL - use WSL1, discussion of WSL2 below) instead of setting up a dual-boot partition.
- Note: there is a choice between WSL1 and WSL2, with the main difference being that WSL2 has significantly improved read-write speeds compared with WSL1 while staying within the Linux file system, but WSL2 has significantly worse read-write speeds when moving between the Linux and Windows file systems. In practical terms, this means that the Linux-based software (OpenFOAM, FEniCS) will read and write faster, at the expense of Windows-based ParaView installations loading results much slower when post-processing. Since OpenFOAM spends significantly more time solving equations than reading and writing files, and gigabytes of data need to be loaded across file systems for post-processing in Windows, I recommend sticking with WSL1. If you prefer WSL2, you can install ParaView on Ubuntu, installing XMing to view the GUI (see this page and this page for further information)
Install OpenFOAM on Ubuntu
The Ubuntu installation instructions as of 31/12/2021 are summarised below (adapted from this website):
curl -s https://dl.openfoam.com/add-debian-repo.sh | sudo bash
sudo apt-get install openfoam2012-defaultEnsure that your ~/.bashrc file has the following line appended (with XXXX replaced with your version number):
source /usr/lib/openfoam/openfoamXXXX/etc/bashrcRestart your Ubuntu. Now check the installation completed correctly by running a tutorial case:
cd ~
mkdir -p OpenFOAM-sims/tutorials
cp -r $FOAM_TUTORIALS/incompressible OpenFOAM-sims/tutorials
cd OpenFOAM-sims/tutorials/incompressible/icoFoam/cavity/cavity/
blockMesh > log.blockMesh
icoFoam > log.icoFoamNote: I use OpenFOAMv2012, but later versions should also work.
Install FEniCS on Ubuntu
The Ubuntu installation instructions as of 31/12/2021 are summarised below (adapted from this website):
sudo apt-get install software-properties-common
sudo add-apt-repository ppa:fenics-packages/fenics
sudo apt-get update
sudo apt-get install fenicsInstall preCICE on Ubuntu
The Ubuntu installation instructions as of 31/12/2021 are summarised below (adapted from this website):
sudo apt update
sudo apt install build-essential cmake libeigen3-dev libxml2-dev libboost-all-dev petsc-dev python3-dev python3-numpy
cd ~
mkdir FSI
cd FSINow either install the Ubuntu package directly with the instructions below (which did not work for me)...
wget https://github.com/precice/precice/releases/download/v2.3.0/libprecice2_2.3.0_focal.deb
sudo apt install ./libprecice2_2.3.0_focal.deb... or install from source:
tar -xzf v2.3.0.tar.gz
cd precice-2.3.0
mkdir build
cd build
cmake -DBUILD_SHARED_LIBS=ON -DCMAKE_BUILD_TYPE=Release -DCMAKE_INSTALL_PREFIX=~/FSI/precice-2.3.0 -DPRECICE_MPICommunication=ON .. ### IMPORTANT! INCLUDE THE TWO DOTS!
make -j 4Test that the cmake command worked as expected:
cd ~/FSI/precice-2.3.0/build
ctest --output-on-failureIf no errors were shown, install the software and test it worked:
make install
make test_installNote: I used preCICE v2.3.0, but later versions should also work.
Install the OpenFOAM-preCICE adapter
The Ubuntu installation instructions as of 31/12/2021 are summarised below (adapted from this website):
cd ~/FSI
wget https://github.com/precice/openfoam-adapter/releases/download/v1.0.0/openfoam-adapter_v1.0.0_OpenFOAMv1812-v2012.tar.gz
tar -xzf openfoam-adapter_v1.0.0_OpenFOAMv1812-v2012.tar.gz
cd openfoam-adapter_v1.0.0_OpenFOAMv1812-v2012/
export LD_LIBRARY_PATH=/usr/lib/x86_64-linux-gnu:$LD_LIBRARY_PATH ### This line may-or-may-not be needed. YMMV.
./AllwmakeNote: this is for OpenFOAMv2012. Please see the preCICE website for information on adapters for later versions.
Install the FEniCS-preCICE adapter
The Ubuntu installation instructions as of 31/12/2021 are summarised below (adapted from this website). This requires Python3, which should already be installed if you followed my previous instructions:
(optional, should not need this line) python3 -m pip install scipy
python3 -m pip install --user fenicspreciceTest the installation ran correctly
... by running this tutorial case:
cd ~/FSI
git clone --branch=master --depth 1 https://github.com/precice/tutorials.git
cd ~/FSI/tutorials/perpendicular-flap/fluid-openfoam
./run.shThe command line output should have paused after this output. If it did not pause, something went wrong.
---[precice] I am participant "Fluid"
---[precice] Setting up master communication to coupling partner/sNow open another Ubuntu terminal, and run these commands:
cd ~/FSI/tutorials/perpendicular-flap/solid-fenics
./run.shBoth terminals should now have log outputs flying. After around 1 minute of computation, both terminals should finish at (roughly) the same time. You can view the results with the following commands, assuming you have installed ParaView on Windows and added the folder containing its .exe file to the Windows PATH environment variable:
cd ~/FSI/tutorials/perpendicular-flap/fluid-openfoam
paraview.exe fluid-openfoam.foamCongratulations! You should now have a functional FSI installation.
Note that as of 31/12/2021, the unmodified FEniCS-preCICE adapter only works in 2D, so you will have to edit the adapter (or download my edited version, TODO add link here) in order to add 3D FSI functionality. Or just wait a few months until I get around to submitting a pull request for my version.
TODO:
- ParaView install instructions
- Resources for learning CFD and FEM
- A complete line-by-line breakdown of simpleFoam
- rhoCentralFoam resources
- rhoCentralFoam rotating reference frame
- Tips and Tricks from experience
- How to do 3D hypersonic fin flutter